Jules Richard
Jules Richard (born 12 August 1862 in Blet, Département Cher, died 14 October 1956 in Châteauroux, Département Indre) was a French mathematician.
Contents |
Life and Works
Richard taught at the lycées of Tours, Dijon and Châteauroux. He obtained his doctorate, at age of 39, from the Faculté des Sciences in Paris. His thesis of 126 pages concerns Fresnel's wave-surface. Richard worked mainly on the foundations of mathematics and geometry, relating to works by Hilbert, von Staudt and Méray.
In a more philosophical treatise about the nature of axioms of geometry Richard discusses and rejects the following basic principles:
- (1) Geometry is founded on arbitrarily chosen axioms - there are infinitely many equally true geometries.
- (2) Experience provides the axioms of geometry, the basis is experimental, the development deductive.
- (3) The axioms of geometry are definitions (in contrast to (1)).
- (4) Axioms are neither experimental nor arbitrary, they force themselves on us since without them experience is not possible.
The latter approach was essentially that proposed by Kant. Richard arrived at the result that the notion of identity of two objects and the invariability of an object are too vague and need to be specified more precisely. This should be done by axioms.
- Axioms are propositions, the task of which is to make precise the notion of identity of two objects pre-existing in our mind.
Further according to Richard, it is the aim of science to explain the material universe. And although non-Euclidean geometry had not found any applications (Albert Einstein finished his general theory of relativity only in 1915), Richard already stated clairvoyantly:
- One sees that having admitted the notion of angle, one is free to choose the notion of straight line in such a way that one or another of the three geometries is true.
Richard corresponded with Giuseppe Peano and Henri Poincaré. He became known to more than a small group of specialists by formulating his paradox which was extensively use by Poincaré to attack set theory whereupon the advocates of set theory had to refute these attacks.
Richard's Paradox
The paradox was first stated in 1905 in a letter to Louis Olivier, director of the Revue générale des sciences pures et appliquées. It was published in 1905 in the article Les Principes des mathématiques et le problème des ensembles. The Principia Mathematica by Alfred North Whitehead and Bertrand Russell quote it together with six other paradoxes concerning the problem of self-reference. In one of the most important compendia of mathematical logic, compiled by Jean van Heijenoort, Richard's article is translated into English. The paradox can be interpreted as an application of Cantor's diagonal argument. It inspired Kurt Gödel and Alan Turing to their famous works. Kurt Gödel considered his incompleteness theorem as analogous to Richard's paradox which, in the original version runs as follows:
Let E be the set of real numbers that can be defined by a finite number of words. This set is denumerable. Let p be the nth decimal of the nth number of the set E; we form a number N having zero for the integral part and p + 1 for the nth decimal, if p is not equal either to 8 or 9, and unity in the contrary case. This number N does not belong to the set E because it differs from any number of this set, namely from the nth number by the nth digit. But N has been defined by a finite number of words. It should therefore belong to the set E. That is a contradiction.
Richard never presented his paradox in another form, but meanwhile there exist several different versions, some of which being only very loosely connected to the original. For the sake of completeness they may be stated here.
Other versions of Richard's Paradox
(A) The version given in Principia Mathematica by Whitehead and Russell is similar to Richard's original version, alas not quite as exact. Here only the digit 9 is replaced by the digit 0, such that identities like 1.000... = 0.999... can spoil the result.
(B) Berry's Paradox, first mentioned in the Principia Mathematica as fifth of seven paradoxes, is credited to Mr. G. G. Berry of the Bodleian Library. It uses the least integer not nameable in fewer than nineteen syllables; in fact, in English it denotes 111,777. But "the least integer not nameable in fewer than nineteen syllables" is itself a name consisting of eighteen syllables; hence the least integer not nameable in fewer than nineteen syllables can be named in eighteen syllables, which is a contradiction
(C) Berry's Paradox with letters instead of syllables is often related to the set of all natural numbers which can be defined by less than 100 (or any other large number) letters. As the natural numbers are a well-ordered set there must be the least number which cannot be defined by less than 100 letters. But this number was just defined by 65 letters including spaces.
(D) König's Paradox was also published in 1905 by Julius König. All real numbers which can be defined by a finite number of words form a subset of the real numbers. If the real numbers can be well-ordered, then there must be a first real number (according to this order) which cannot be defined by a finite number of words. But the first real number which cannot be defined by a finite number of words has just been defined by a finite number of words.
(E) The smallest natural number without interesting properties acquires an interesting property by this very lack of any interesting properties.
(F) A loan of the Paradox of Grelling and Nelson. The number of all finite definitions is countable. In lexical order we obtain a sequence of definitions D1, D2, D3, ... Now, it may happen that a definition defines its own number. This would be the case if D1 read "the smallest natural number". It may happen, that a definition does not describe its own number. This would be the case if D2 read "the smallest natural number". Also the sentence "this definition does not describe its number" is a finite definition. Let it be Dn. Is n described by Dn. If yes, then no, and if no, then yes. The dilemma is irresolvable. (This version is described in more detail in another article, Richard's paradox.)
Reactions to Richard's Paradox
Georg Cantor wrote in a letter to David Hilbert:
- "Infinite definitions" (i.e., definitions which cannot be done in finite time) are absurdities. If Königs statement was "correct", according to which all "finitely definable" real numbers form a collection of cardinal number
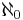 , this would imply the countability of the whole continuum; but this is obviously wrong. The question is now what error the alleged proof of his wrong theorem is based upon. The error (which also appears in the note of a Mr. Richard in the last issue of the Acta mathematica, which Mr. Poincaré emphasizes in the last issue of the Revue de Métaphysique et de Morale) is, in my opinion, the following: It is assumed that the system {B} of notions B, which have to be used for the definition of individual numbers, is at most countably infinite. This assumption "must be in error" because otherwise we would have the wrong theorem: "the continuum of numbers has cardinality
, this would imply the countability of the whole continuum; but this is obviously wrong. The question is now what error the alleged proof of his wrong theorem is based upon. The error (which also appears in the note of a Mr. Richard in the last issue of the Acta mathematica, which Mr. Poincaré emphasizes in the last issue of the Revue de Métaphysique et de Morale) is, in my opinion, the following: It is assumed that the system {B} of notions B, which have to be used for the definition of individual numbers, is at most countably infinite. This assumption "must be in error" because otherwise we would have the wrong theorem: "the continuum of numbers has cardinality 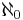 ".
".
Here Cantor is in error. Today we know that there are uncountably many real numbers without the possibility of a finite definition.
Ernst Zermelo comments Richard's argument:
- The notion "finitely definable" is not an absolute one but a relative one being always related to the "language" chosen. The conclusion according to which all finitely definable objects are countable is only valid in case that one and the same system of symbols is used; the question whether a single individual can be subject to a finite definition is void because to every thing an arbitrary name can be attached to.
Zermelo points to the reason why Richard's paradox fails. His last statement, however, is impossible to satisfy. A real number with infinitely many digits, which are not determined by some "rule", has an infinitely large contents of information. Such a number could only be identified by a short name if there were only one or few of them existing. If there exist uncountably many, as is the case, an identification is impossible.
Papers and Books by Jules Richard
- Thèses présentées à la Faculté des sciences de Paris par M. Jules Richard, 1re thèse: Sur la surface des ondes de Fresnel..., Chateauroux 1901 (126 pages).
- Sur la philosophie des mathématiques, Gauthier-Villars, Paris 1903 (248 pages).
- Sur une manière d'exposer la géométrie projective, L'Enseignement mathématique 7 (1905) 366-374.
- Les principes des mathématiques et le problème des ensembles, Revue générale des sciences pures et appliquées 16 (1905) 541-543.
- The principles of mathematics and the problem of sets (1905), English translation in Jean van Heijenoort, "From Frege to Gödel - A Source Book in Mathematical Logic", 1879-1931. Harvard Univ. Press, 1967, p. 142-144.
- Lettre à Monsieur le rédacteur de la Revue Générale des Sciences, Acta Math. 30 (1906) 295-296.
- Sur les principes de la mécanique, L'Enseignement mathématique 8 (1906) 137-143.
- Considérations sur l'astronomie, sa place insuffisante dans les divers degrés de l'enseignement, L'Enseignement mathématique 8 (1906) 208-216.
- Sur la logique et la notion de nombre entier, L'Enseignement mathématique 9 (1907 ) 39-44.
- Sur un paradoxe de la théorie des ensembles et sur l'axiome Zermelo, L'Enseignement mathématique 9 (1907) 94-98.
- Sur la nature des axiomes de la géométrie, L'Enseignement mathématique 10 (1908 ) 60-65.
- Sur les translations, L'Enseignement mathématique 11 (1909) 98-101.
- Contre la géométrie expérimentale Revue de l’Enseignement des Sciences (1910) 150.
Literature and Links for Biographical Data
- J. Itard: Richard, Jules Antoine, Dictionary of Scientific Biography, 11, Charles Scribner's Sons, New York (1980) 413-414.
[This seems to be the only original source, used by all other biographers.]
- S. Gottwald: Richard, Jules Antoine in: Lexikon bedeutender Mathematiker, Harri Deutsch, Thun und Frankfurt (M) 1990.
- J. J. O'Connor, E. F. Robertson: The MacTutor History of Mathematics archive [1]
- fr:Jules Richard
- [2]
- [3]
Literature and Links for the Paradox
- H. Meschkowski, W. Nilson: Georg Cantor - Briefe, Sphinhubyringer, Berlin 1991, p. 446.
- W. Mückenheim: Die Mathematik des Unendlichen, Shaker, Aachen 2006.
- A. N. Whitehead, B. Russell: Principia Mathematica I, Cambridge Univ. Press, Cambridge 1910, p. 64. [4]
- E. Zermelo: Neuer Beweis für die Möglichkeit einer Wohlordnung, Math. Ann. 65 (1908) p. 107-128. [5]
- Proof of impossibility
- fr:Paradoxe de Richard
- fr:Paradoxe de Berry
- [6]
- [7]
- [8]
- [9]
Final remark: The mathematician Jules Richard is not identical with the publicist (* 1810, † 1868) and also not with the manufacturer of scientific instruments and founder of the lycée technique Jules Richard in Paris (* 1848, † 1930). In the big encyclopedias and diaries of scholars the name Jules Richard is missing - even in the French ones. Therefore his biographical data are rather scanty.